B Appendix B: Secure Remote Password

In “A modern approach to authentication,” we spoke of mathematical magic.

Using some mathematical magic the server and the client are able to send each other puzzles that can only be solved with knowledge of the appropriate secrets, but no secrets are transmitted during this exchange.

This appendix offers some insight into that magic.

We insist on this magic even though 1Password’s principle source of security is through end-to-endData is only encrypted or decrypted locally on the users’ devices with keys that only the end users possess. This protects the data confidentiality and integrity from compromises during transport or remote storage. encryption instead of authentication. We need to ensure our authentication system would never provide an attacker the means to learn anything about the secrets needed to decrypt someone’s data — even if it were compromised.

We use Secure Remote Password (SRP)A method for both a client and server to authenticate each other without either revealing any secrets. In the process, they also agree on an encryption key to be used for the current session. We’re using Version 6 with a modified key derivation function. as our password-authenticated key exchange (PAKE)Password-based key exchange protocol allows for a client and server to mutually authenticate each other and establish a key for their session. It relies on either a secret each have or related secrets that each have. to achieve the authentication goals set out in Figure 4.1. With SRP, the client can compute from a password (and a few other things) a number that is imaginatively called $x$. This secret $x$ is never transmitted.

B.0.1 Registration

The client computes $x$ from the user’s account passwordSomething you must remember and type when unlocking 1Password. It’s never transmitted from your devices. Previously known as Master Password. and Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key. and from some non-secret information as described in section B.0.3.

During first registration, the client will compute from $x$ a verifier, $v$. During initial registration, the client sends $v$ to the server, along with a non-secret saltA non-secret value added to either an encryption process or hashing to ensure the result of the encryption is unique. Salts are typically random and unique.. The client and the server also need to agree on some other non-secret parameters. The verifier is the only sensitive information ever transmitted, and it’s sent only during initial registration.

Dangerous bend

The verifier $v$ cannot be used directly to compute either $x$ or the password that was used to generate $x$; however, it’s similar to a password hash in that it can be used in password cracking attempts. That is, an attacker who has acquired $v$ can make a password guess and see if processing that guess yields an $x$ that produces the $v$. Our use of two-secret key derivation (2SKD)Two different secrets, each with their own security properties, are used in deriving encryption and authentication keys. In 1Password, these are your account password (something you know) and your Secret Key (a high-entropy secret you have on your device). makes it impossible to launch such a cracking attack without also having the user’s Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key..

B.0.2 Sign-in

The client will be able to compute $x$ from the account passwordSomething you must remember and type when unlocking 1Password. It’s never transmitted from your devices. Previously known as Master Password., Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key., and saltA non-secret value added to either an encryption process or hashing to ensure the result of the encryption is unique. Salts are typically random and unique. as described in 8.2.³⁹ The server has $v$. Because of the special relationship between $x$ and $v$, the server and client can present each other mathematical challenges that achieve the following:

Prove to the server the client has the $x$ associated with $v$.
Prove to the client the server has the $v$ associated with $x$.
Let the client and server agree on a key $S$ which can be used for further encrypting the session.

During that exchange, no information about the user’s password is revealed, nor is any information about $x$ or $v$ or $S$ revealed to someone listening in. Furthermore, the mathematical challenge the client and server present to each other is different each time, so one session cannot be replayed.

B.0.3 With a strong KDF

The standards documents describing SRPA method for both a client and server to authenticate each other without either revealing any secrets. In the process, they also agree on an encryption key to be used for the current session. We’re using Version 6 with a modified key derivation function. offer the generation of $x$ from the password, $P$; salt, $s$; and username, $I$; as in Figure B.1. The values of $g$ and $N$ are public parameters that will be further described in B.1.

Figure B.1: Deriving 𝑥 and 𝑣 as given in RFC 5054, where H represents a cryptographic hash function (for example, SHA256).

Although it’s infeasibleEffectively impossible. It’s not technically impossible for a single monkey placed in front of a manual typewriter for six weeks to produce the complete works of Shakespeare. It is, however, infeasible, meaning that the probability of it happening is so outrageously low that can be treated as impossible. to compute $P$ from $x$ or $x$ from $v$, it’s possible to use knowledge of $v$ (and the public parameters) to test a candidate password, $P'$. All an opponent needs to do is compute $v'$ from $P'$ and see if $v'$ equals $v$. If $v' = v$ then the guessed password $P'$ is (almost certainly) the correct password.

As discussed elsewhere, we offer three defenses against such an attack if an attacker obtains $v$ (which is stored on our server and transmitted during initial registrations).

We use two-secret key derivation (2SKD)Two different secrets, each with their own security properties, are used in deriving encryption and authentication keys. In 1Password, these are your account password (something you know) and your Secret Key (a high-entropy secret you have on your device). with the completely random Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key. as one of the secrets in deriving $x$. Password cracking isn’t a feasible approach for an attacker without the Secret Key. For a discussion of this point, see 3.2.
We use a slower key derivation function for deriving $x$ than the one shown in Figure B.1, so even if an attacker obtains both $v$ and the user’s Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key., each guess is computationally expensive.
We encourage the use of strong account passwords. Thus an attacker who has both $v$ and the account passwordSomething you must remember and type when unlocking 1Password. It’s never transmitted from your devices. Previously known as Master Password. will need to make a very large number of guesses.

The latter two mechanisms come into play only if the Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key. is acquired from the user’s device.

It should be noted that although the password processing shown in Figure B.1 is presented in RFC 5054⁴⁰, the standard does not insist on it. Indeed, RFC 5054 refers to RFC 2954⁴¹ S3.1 which states

SRP can be used with hash functions other than [SHA1]. If the hash function produces an output of a different length than [SHA1] (20 bytes), it may change the length of some of the messages in the protocol, but the fundamental operation will be unaffected…

Any hash function used with SRP should produce an output of at least 16 bytes and have the property that small changes in the input cause significant nonlinear changes in the output. [SRP] covers these issues in more depth.

So in our usage, we compute $x$ using the key derivation method described in detail in 8.2.

B.1 The math of SRP

B.1.1 Math background

The client will have its derived secret $x$, and the server will have its verifier, $v$. The mathematics that allow for the client and server to mutually authenticate and arrive at a key without exposing either secret is an extension of Diffie-Hellman key exchange (DHE)An application of the discrete logarithm problem (DLP) to provide a way for parties to decide upon a secret key without revealing any secrets during the communication. It’s named after Whitfield Diffie and Martin Hellman who published it in 1976.. This key exchange protocol is, in turn, based on the discrete logarithm problem (DLP)If 𝑦≡𝑔𝑥 mod𝑝 (for a carefully chosen𝑝and some other conditions) it’s possible to perform exponentiation to compute 𝑦 from the other variables, but it’s thought to be infeasible to compute 𝑥 from 𝑦. Computing 𝑥 from 𝑦 (and the other parameters) is reversing the exponentiation and is taking a logarithm..

Recall (or relearn) from high school math:

\[\begin{equation} (b^n)^m = b^{nm}\tag{B.1} \end{equation}\]

Equation (B.1) holds true even if we restrict ourselves to integers and do all of this exponentiation modulo some number $N$.

The crux of the DLPIf 𝑦≡𝑔𝑥 mod𝑝 (for a carefully chosen𝑝and some other conditions) it’s possible to perform exponentiation to compute 𝑦 from the other variables, but it’s thought to be infeasible to compute 𝑥 from 𝑦. Computing 𝑥 from 𝑦 (and the other parameters) is reversing the exponentiation and is taking a logarithm. is that if we pick $N$ and $g$ appropriately in equation (B.2)

\[\begin{equation} v = g^x (\text{mod} N) \tag{B.2} \end{equation}\]

It’s easy (for a computer) to calculate $v$ when given $x$, but infeasibleEffectively impossible. It’s not technically impossible for a single monkey placed in front of a manual typewriter for six weeks to produce the complete works of Shakespeare. It is, however, infeasible, meaning that the probability of it happening is so outrageously low that can be treated as impossible. to compute $x$ when given $v$.

Calculating $x$ from $v$ (given $g$ and $N$) is computing the discrete logarithm of $v$. To ensure calculating the discrete logarithm is, indeed, infeasible, $N$ must be chosen carefully. The particular values of $N$ and $g$ used in 1Password are drawn from the groups defined in RFC 3526.⁴² Given current and anticipated computing power, $N$ should be at least 2048 bits.

Sophie Germain (1776--1831) proved that Fermat's Last Theorem holds for exponents $n = 2q + 1$ where both $q$ and $n$ are prime. Primes like $q$ are now called “Sophie Germain primes.” Germain stole the identity of a male mathematics dropout to enter into correspondence with mathematicians in France and elsewhere in Europe. It's only after they'd come to respect her work that she could reveal her true identity. Her fame at the time was mostly for her work in mathematical physics, but it her work in number theory that plays a role in cryptography today.

Figure B.2: Sophie Germain (1776–1831) proved that Fermat’s Last Theorem holds for exponents $n = 2q + 1$ where both $q$ and $n$ are prime. Primes like $q$ are now called “Sophie Germain primes.” Germain stole the identity of a male mathematics dropout to enter into correspondence with mathematicians in France and elsewhere in Europe. It’s only after they’d come to respect her work that she could reveal her true identity. Her fame at the time was mostly for her work in mathematical physics, but it her work in number theory that plays a role in cryptography today.

B.1.2 Diffie-Hellman key exchange

If Alice and Bob have agreed on some $g$ and $N$, neither of which need to be secret, Alice can pick a secret random number $a$ and calculate $A = g^a (\text{mod} N)$. Bob can pick his own secret, $b$, and calculate $B = g^b (\text{mod} N)$. Alice can send $A$ to Bob, and Bob can send $B$ to Alice.

Assuming an appropriate $N$ and $g$, Alice won’t be able to determine Bob’s secret exponent $b$, and Bob won’t be able to determine Alice’s secret exponent $a$. No one listening in – even with full knowledge of $g$, $N$, $A$, and $B$ – will be able to determine $a$ or $b$.⁴³ There is, however, something that both Alice and Bob can calculate that no one else can. In what follows, it goes without saying (or writing) that all operations are performed modulo $N$.

Alice can compute:

\[\begin{equation} S=B^a \tag{B.3} \end{equation}\] \[\begin{equation} = (g^b)^a\ \ \ \ \ \ \ because\ \ 𝐵=𝑔^b \end{equation}\] \[\begin{equation} = g^{ba}\ \ \ \ \ \ \ because\ \ (B.1) \tag{B.4} \end{equation}\]

Equation (B.3) is what Alice actually computes because she knows her secret $a$ and has been given Bob’s public exponent. But note that the secret, $S$, that Alice computes is the same as what we see in (B.4).

Bob can compute:

\[\begin{equation} S = A^b \end{equation}\] \[\begin{equation} = (g^a)^b\ \ \ \ \ \ \ because\ \ A = g^a \end{equation}\] \[\begin{equation} = g^{ab}\ \ \ \ \ \ \ because\ \ (B.1) \tag{B.5} \end{equation}\]

From equations (B.5) and (B.4) we see that both Alice and Bob are computing the same secret, $S$. They do so without revealing any secrets to each other or anyone listening in.

We use the session key, $S$, as an additional encryption and authentication layer on the client/server communication for that session. This is in addition to the encryption and authentication provided by TLS and the authenticated encryption of the user data.

All the secrets used and derived during DHEAn application of the discrete logarithm problem (DLP) to provide a way for parties to decide upon a secret key without revealing any secrets during the communication. It’s named after Whitfield Diffie and Martin Hellman who published it in 1976. are ephemeral: They’re created for the individual session alone. Alice will create a new $a$ for each session; Bob will create a new $b$ for each session; the derived session key, $S$, will be unique to that session. One advantage of this is that a successful break of these secrets by some attacker will allow the attacker to decrypt the messages of that session only.

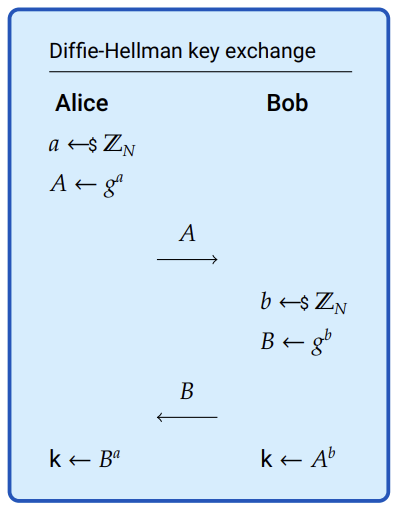
In Diffie-Hellman key exchange, $N$ and $g$ are already known to all parties and all exponentiation is done $mod N$. The form given here is somewhat less general than it could be in order to avoid having to introduce more notation and abstractions.

Figure B.3: In Diffie-Hellman key exchange, $N$ and $g$ are already known to all parties and all exponentiation is done $mod N$. The form given here is somewhat less general than it could be in order to avoid having to introduce more notation and abstractions.

B.1.3 Authenticated key exchange

DHEAn application of the discrete logarithm problem (DLP) to provide a way for parties to decide upon a secret key without revealing any secrets during the communication. It’s named after Whitfield Diffie and Martin Hellman who published it in 1976., as described in the previous section, allows Alice and Bob to agree on an encryption key for their communication. It doesn’t, however, include a mechanism by which either Alice or Bob can prove to the other they are Alice and Bob. Our goal, however, is to have mutual authenticationMutual authentication is a process in which all parties prove their identity to each other. between the 1Password client and server.

In order for Alice to prove to Bob she’s the same “Alice” he has corresponded with previously, she needs to hold (or regenerate) a long-term secret. At the same time, we don’t want to transmit any secrets during authentication.

SRPA method for both a client and server to authenticate each other without either revealing any secrets. In the process, they also agree on an encryption key to be used for the current session. We’re using Version 6 with a modified key derivation function. builds upon DHEAn application of the discrete logarithm problem (DLP) to provide a way for parties to decide upon a secret key without revealing any secrets during the communication. It’s named after Whitfield Diffie and Martin Hellman who published it in 1976., but adds two long-term secrets. $x$ is held (or regenerated) by the client and $v$, the verifier, is stored by the server. The verifier is created by the client from $x$ and transmitted only during initial enrollment, and that’s the only time a secret is transmitted.

As described in detail in “Key derivation,” $x$ is derived from a account passwordSomething you must remember and type when unlocking 1Password. It’s never transmitted from your devices. Previously known as Master Password. and Secret KeyA randomly generated user secret key that is created upon first signup. It’s created and stored locally. Along with the user’s account password, it’s required both for decrypting data and for authenticating to the server. The Secret Key prevents an attacker who has acquired remotely stored data from attempting to guess a user’s account password. Previously known as the Account Key.. The client computes $v = g^x$ and sends $v$ to the server during initial enrollment.

During a normal sign-in, the client picks a secret random number $a$ and computes $A = g^a$ as described above in “Diffie-Hellman key exchange”. It sends $A$ to the server (along with its email address).

The server picks a random number, $b$, but unlike unauthenticated DHEAn application of the discrete logarithm problem (DLP) to provide a way for parties to decide upon a secret key without revealing any secrets during the communication. It’s named after Whitfield Diffie and Martin Hellman who published it in 1976., it computes $B$ as $B = kv + g^b$ and sends that to the client.

Everyone (including a possible attacker) can now compute a non-secret $u$ from $A$ and $B$ by using a hash.⁴⁴ The server will calculate a raw $S$ as

\[\begin{equation} S = {\left(Av^u\right)}^b \end{equation}\] The client will calculate the same raw $S$ as \[\begin{equation} S = {\left(B - kg^x\right)}^{a + ux} \end{equation}\]

The client and server will calculate the the same raw $S$ if $v$ is constructed from $x$ as in equation (B.2) and $A$ and $B$ are constructed as described above. The proof is left as an exercise to the reader. (And the proof this is the only feasible way for the values to be the same is left for advanced texts.)

The client may locally store $x$ in a way that’s encrypted with keys that depend on the Account Unlock Key (AUK)Key used to decrypt a user’s personal key set. It’s derived from the user’s account password and Secret Key. Previously known as the Master Unlock Key. instead of recalculating it afresh each time.↩︎
Taylor et al. (2007)↩︎
Rehbehn and Fowler (2000)↩︎
Kivinen and Kojo (2003)↩︎
There are numerous mathematical assumptions behind the claim that it’s infeasible to determine $a$ from $A$. Mathematicians are confident that some things involved are “hard” to compute but lack full mathematical proof. There are also some physical assumptions behind the security claims. We know the relevant computations we want to be difficult are not hard using large quantum computers of a certain sort. We’re assuming, with some justification, that constructing the appropriate sort of quantum computer is beyond anyone’s reach for at least a decade. We anticipate the development of post-quantum cryptographic algorithms over the next decade or so, but nothing is yet suitably mature to be of use to us now.↩︎
It doesn’t matter too much how $u$ is created, but it must be standardized so the server and client do it the same way. We use the SHA256 hash of $A | B$.↩︎